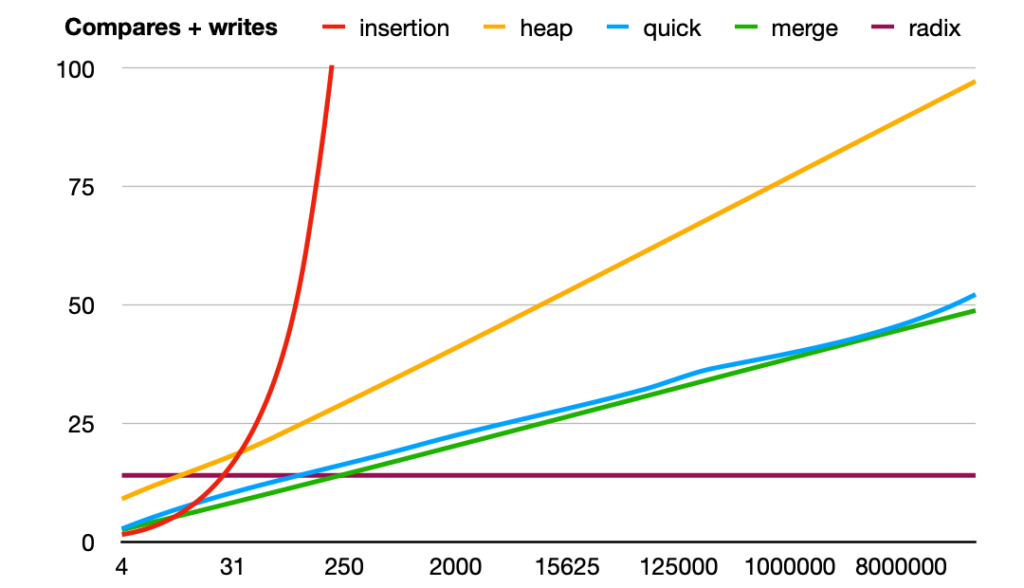
Complexities of Sorting Techniques: Quick Sort vs Merge Sort vs Bubble Sort 2025

int

Sorting algorithms are a cornerstone of computer science, forming the basis for efficient data organization and retrieval. Understanding the complexities of sorting techniques is crucial for developers, data scientists, and computer science students alike. Among the most widely studied sorting methods are Quick Sort, Merge Sort, and Bubble Sort. Each comes with its own strengths, weaknesses, and time-space trade-offs. This article explores their complexities, practical use cases, and comparative performance. complexities of sorting techniques

Quick Sort: Efficient Yet Tricky

Quick Sort is a divide-and-conquer algorithm that works by selecting a ‘pivot’ element and partitioning the array into elements less than and greater than the pivot. This process repeats recursively on the subarrays. When implemented well, Quick Sort is extremely fast and memory-efficient.

Time Complexity: In the best and average cases, Quick Sort operates in O(n log n) time. However, its worst-case time complexity is O(n^2), which occurs when the pivot selection leads to highly unbalanced partitions. complexities of sorting techniques

Space Complexity: Quick Sort is generally in-place, using O(log n) auxiliary space due to recursive calls. This makes it space-efficient compared to Merge Sort. complexities of sorting techniques

Quick Sort is ideal for large datasets where performance matters, especially in environments where memory is a constraint. However, it is sensitive to input data order and pivot selection strategy, which can significantly affect performance. Techniques like randomized pivot selection or the median-of-three approach can help mitigate the worst-case scenario. complexities of sorting techniques

Merge Sort: Stable and Predictable

Merge Sort is another divide-and-conquer algorithm that splits the array into halves, recursively sorts them, and merges the sorted halves back together. It’s known for its consistent performance and stability, which makes it suitable for sorting linked lists and datasets where the order of equal elements must be preserved. complexities of sorting techniques complexities of sorting techniques

Time Complexity: Merge Sort has a predictable time complexity of O(n log n) in all cases—best, average, and worst. This reliability makes it an attractive choice when performance consistency is crucial. complexities of sorting techniques complexities of sorting techniques

Space Complexity: Merge Sort requires O(n) additional space for temporary arrays used in merging. While this is a drawback for large datasets in constrained environments, the trade-off is acceptable in many applications where stability and predictability are more important than raw speed. complexities of sorting techniques

Merge Sort is commonly used in scenarios where stability is essential, such as database sorting or when working with linked data structures. Its parallelizability also makes it a strong candidate for distributed computing tasks. complexities of sorting techniques

Bubble Sort: Simple but Inefficient

Bubble Sort is often the first sorting algorithm taught in introductory programming courses due to its simplicity. It repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. Despite its intuitive nature, Bubble Sort is rarely used in real-world applications because of its inefficiency. complexities of sorting techniques

Time Complexity: Bubble Sort has a worst-case and average-case time complexity of O(n^2), making it impractical for large datasets. In the best-case scenario, where the list is already sorted, it runs in O(n) time with an optimized implementation that checks for early termination. complexities of sorting techniques

Space Complexity: It operates in-place with O(1) auxiliary space, which is a positive aspect. However, this minimal space usage doesn’t compensate for its poor time performance. complexities of sorting techniques

Bubble Sort is mostly used for educational purposes or in cases where simplicity outweighs performance. It’s a good tool for demonstrating the basic principles of sorting and algorithmic thinking but is almost never the best choice for production code. complexities of sorting techniques

Comparative Analysis: Choosing the Right Tool

Understanding the complexities of sorting techniques helps in choosing the right algorithm based on the problem at hand. Quick Sort is usually the fastest in practice for general-purpose sorting but is less predictable. Merge Sort offers guaranteed performance and stability, making it a better choice in applications where consistency is key. Bubble Sort, while conceptually useful, is generally avoided in performance-critical scenarios. complexities of sorting techniques

When working with massive datasets, consider hybrid algorithms like Timsort (used in Python), which combine the strengths of Merge Sort and Insertion Sort for optimal performance. Understanding the theoretical and practical aspects of sorting algorithm complexities equips you with the tools to write more efficient and scalable code.

Conclusion: Mastering Sorting Complexities

Mastering the complexities of sorting techniques is not just about memorizing time and space complexities. It’s about understanding the nuances of each algorithm—how they behave with different data, how they manage memory, and how they scale. Whether you’re preparing for coding interviews, optimizing backend performance, or studying algorithm design, knowing when and why to use Quick Sort, Merge Sort, or even Bubble Sort can make a significant difference.

In the world of algorithms, there’s no one-size-fits-all. Each sorting technique brings something unique to the table. By aligning algorithm choice with the specific needs of your application, you not only write better code but also build systems that perform reliably and efficiently.